三分钟入门DeepONet

神经网络可以作为通用的函数逼近器。但是还有一个古老的理论——Universal Approximation Theorem for Operator（Chen et al. 1995）表示，神经网络可以被用来逼近数学算子（比如积分，常微分方程ODEs，偏微分方程PDEs），实现函数到函数/实数的映射。为了方便讨论，我们用$G$来表示要拟合的算子，$G(u)(y)$则是经过算子操作得到的新函数在$y$处的值。比如，$G$可以表示对函数$u(x)$做不定积分，$G: u(x) →s(x)=\int_0^xu(\tau)d\tau$。

Approximation Theorem告诉我们可以用神经网络来学习$G$，很自然的，我们可以想到见下图A所表示的神经网络架构，即一股脑将$u$和$y$传给一个神经网络（比如全连接神经网络FNNs），用它替代算子，然后输出$G(u)(y)$。理论上这是可行的，但是这样的神经网络很难训练。为了又快又好的学习$G$，Lu et al.提出了DeepONet的概念，即图C、D。它的架构很简单，由Branch和Trunk两部分组成。Branch的输入为函数$u$，Trunk的输入为$y$，将Branch和Trunk的输入做点成就得到了$G(u)(y)$。

假设我们要训练这个神经网络来求解上面不定积分的问题，首先要考虑的就是如何把连续函数传给神经网络。显然，我们无法告诉神经网络这个函数在整个空间各个点处的值。DeepONet的作者提出了”discrete sensor”的概念，很形象。也就是说，想象我们在一些固定的位置放上传感器，它们可以捕捉函数在这个位置的值。将所有传感器捕捉到的值拼成一个向量，作为神经网络的输入。比如🌰，输入的函数 u(x)=x2 ，我们把sensors定在 x1=2,x2=5,x3=6 这三个位置，获得 u=[4,25,36] 作为神经网络的输入向量。相较于以往的研究，DeepONet的一大亮点就是，这些sensors不一定均匀分布，可以放置在定义域的任何位置，只要所有的训练和测试数据都用同样的sensors就行。

知道了如何表示神经网络的输入，那么如何生成大量的inputs呢？这个问题可以拆分为两部分：(1)选取什么函数空间，(2)如何采样。论文中提到了两个函数空间：Gaussian radom field(GRF)和Chebyshev polynomials。这里只以GRF为🌰。我们可以定义这样的核函数 \(k_l(x_1,x_2)=exp(-\|x_1-x_2\|^2)/2l^2\) 然后通过高斯过程生成$u$ \(u \sim G(0,k_l(x_1,x_2))\) 为了偷懒，这里就不详述了，感兴趣的读者可以参考Görtler el al.的论文“A Visual Exploration of Gaussian Processes”。这里不理解也没关系，总之就是我们创建了包揽了无限多连续函数的篮子，我们可以从中随机抓取函数（见下图）。然后，获取函数在sensors处的值作为DeepONet Branch的输入。 |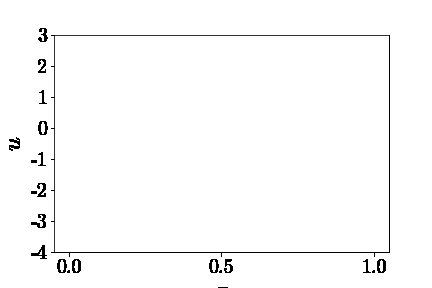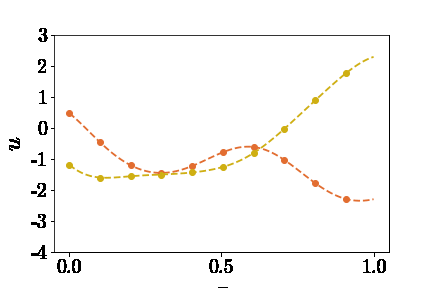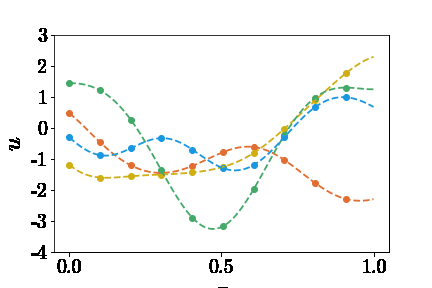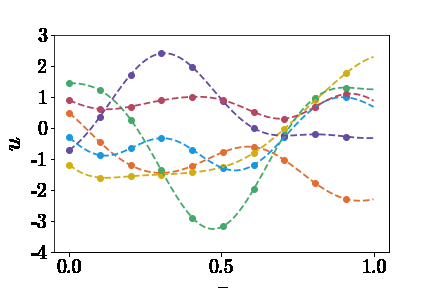 | |:–:| | $u(x)$ |

Trunk部分的输入很简单，就是在定义域内随意取一个或多个坐标$y$，然后求得$G(u)(y)$作为预期输出。 |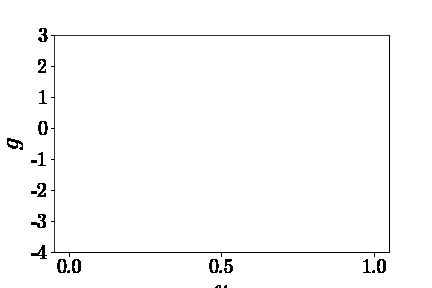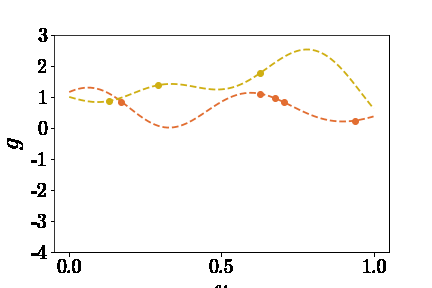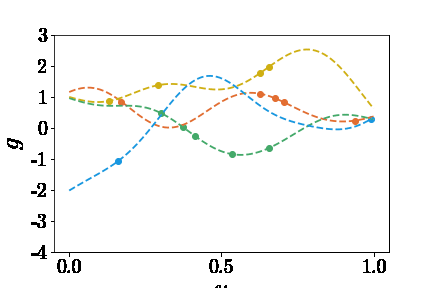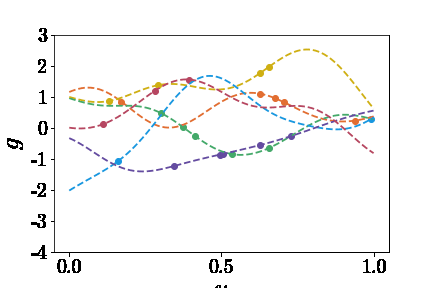 | |:–:| | $G(u)(y)$ |

以黄线为例，给DeepONet的输入和预期输出如下图示

接下来就是一些常规操作，定义loss，optimizer，train，test。。。完整的demo代码见这个链接。

补充：

• DeepONet只是个框架，里面子神经网络不一定非得是FNN。

REFs:

• Görtler, et al., “A Visual Exploration of Gaussian Processes”, Distill, 2019.
• Lu, Lu, Pengzhan Jin, and George Em Karniadakis. ‘DeepONet: Learning Nonlinear Operators for Identifying Differential Equations Based on the Universal Approximation Theorem of Operators’. Nature Machine Intelligence 3, no. 3 (March 2021): 218–29. https://doi.org/10.1038/s42256-021-00302-5.